 |
| Professor Andrew Wiles is seen here with the Fermat's Last Theorem stated on a chalkboard in his Princeton, N.J., office, back in 1998. |
The man who is the focus of this article, Professor Andrew Wiles, a British mathematician, who has gotten to himself loads of fame, prizes and their accompanying monetary rewards, including a knighthood, for taking down a mathematics problem that has enjoyed a reputation for being notoriously hard to attempt, the perfect mathematician's nightmare, for nearly 358 years.
Andrew Wiles was born to British parents on 11th April 1953, in Cambridge, England. He attended King's College School, Cambridge. Wiles obtained both his bachelor's degree and PhD, both from Merton College, Oxford in 1974, and from Clare College, Cambridge, in 1980 respectively. He became a professor of mathematics at Princeton University,
1981, and also a royal society research professor at the university of Oxford. He was also a Eugene Higgins professor, from 1994-2009, and since then have had a pretty active research and academic career. Producing a proof for Fermat's last theorem was one of the major focus of hiss research career.
Wiles first encountered the problem when just ten years old, while he was scouring a library, a theorem put forth by Pierre De Fermat three plus centuries before, 1636 to be precise. Young Wiles' fascination for a mathematical problem he as a ten year-old could understand, yet remaining unsolved up to that point made him resolve to be the first to solve the longstanding mathematical problem that had gain notoriety for upsetting mathematicians through the centuries. Preceding his attack on the mathematical enigma, he studied the works of other people that had attempted the problem, most especially in the 18th and 19th centuries. The likes of the legendary Leonhard Euler and others.
 |
| Pierre de Fermat conjectured the Fermat's Last theorein in 1637. |
Pierre De Fermat, a very important figure in the history of mathematics, put forth a deceptively simple theorem which
states that no three distinct positive integers
a,
b, and
c can satisfy the equation
- {a^{n}+b^{n}=c^{n}}

if
n is an integer greater than two (
n > 2).
Though there are claims that De Fermat himself had provided the proof for his theorem, there no evidences that confirm that except tantalizing notes he left. One of those notes read " I have a truly marvellous demonstration of this proposition, which this margin is too narrow to contain".
While in Cambridge, Wiles had worked with John Coates on the arithmetic of elliptic curves, which They are defined by points in the plane whose co-ordinates

and
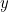
satisfy an equation of the form
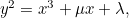
where
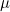
and
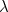
are constants, and they are usually doughnut-shaped or toroidal. At the time of professor Wiles work on elliptic curves they were an area of mathematics unrelated to the Fermat's Last Theorem. It was needful to link elliptic curves, Taniyama- Shimira and the Fermat's Last Theorem. The Tamiyama-Shimura-Weil conjecture, states that every elliptic curve can be matched to a modular form. And so it a huge stroke of luck when a link between Fermat's last theorem and elliptic curves and the Taniyama- Shimura-Weil conjecture was discovered in 1986 by Ken Ribet, who built on the previous work of Gerhard Frey.
Wiles heard the news of Ribet's achievement and it occurred to him that to prove Fermat's last theorem, he need only prove the Taniyama-Shimura-Weil conjecture. Andrew Wiles worked on the theorem to provide an adequate proof for near 7 years, in almost- total secrecy. His hard work paid off , and the proof was presented for the first time at a conference in Cambridge.
Sir Andrews proof was later discovered to contain a flaw, inAugust 1993. The error was corrected after a year of intensive work, thus making Wiles proof of the famous theorem complete. For his groundbreaking achievements, Wiles has been the recipient of numerous awards, including the 2016 Abel prize for mathematics, (considered by some to be the noble prize of mathematics), for which Wiles received 6 million Kroner (US$700,000), plus a place in history among the greatest mathematical minds to ever walk the planet.




 and
and 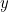 satisfy an equation of the form
satisfy an equation of the form
 and
and  are constants, and they are usually doughnut-shaped or toroidal. At the time of professor Wiles work on elliptic curves they were an area of mathematics unrelated to the Fermat's Last Theorem. It was needful to link elliptic curves, Taniyama- Shimira and the Fermat's Last Theorem. The Tamiyama-Shimura-Weil conjecture, states that every elliptic curve can be matched to a modular form. And so it a huge stroke of luck when a link between Fermat's last theorem and elliptic curves and the Taniyama- Shimura-Weil conjecture was discovered in 1986 by Ken Ribet, who built on the previous work of Gerhard Frey.
are constants, and they are usually doughnut-shaped or toroidal. At the time of professor Wiles work on elliptic curves they were an area of mathematics unrelated to the Fermat's Last Theorem. It was needful to link elliptic curves, Taniyama- Shimira and the Fermat's Last Theorem. The Tamiyama-Shimura-Weil conjecture, states that every elliptic curve can be matched to a modular form. And so it a huge stroke of luck when a link between Fermat's last theorem and elliptic curves and the Taniyama- Shimura-Weil conjecture was discovered in 1986 by Ken Ribet, who built on the previous work of Gerhard Frey.
Comments
Post a Comment